Plaka dinamiklerini geçersiz kılma ile şekillendirilmiş Afar Triple Kavşak’ta Mantle Upwelling

Örnek seçimi ve işleme

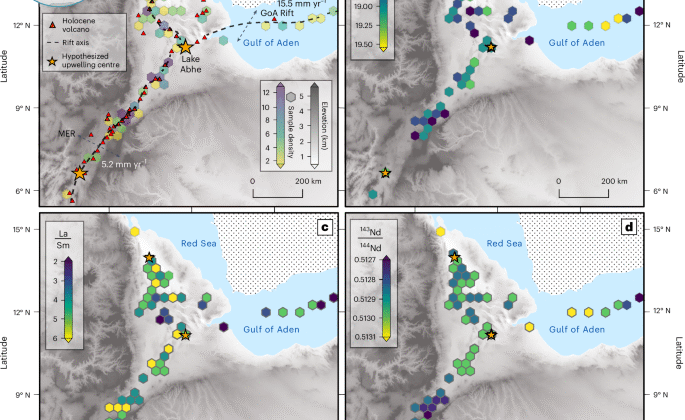
Bu çalışmada kullanılan tüm örnekler ve daha önce yayınlanmış veriler, Holosen içinde aktif olan bir volkandan kaynaklanmalıdır.²¹ (İncir. 1), örneğin kuaterner yaşta (<2.58 mA) olduğu tahmin edilir. Temel bir kriter, tüm numunelerin doğru koordinatlarla tam olarak bilinen bir yere sahip olmasıydı.

Daha önce yayınlanmış verileri elde etmek

Daha önce yayınlanmış jeokimyasal veriler Georoc’tan elde edildi^19–32. İndirildikten sonra, veri dosyaları yalnızca Etiyopya (MER ve Afar dahil) içindeki verileri içerecek şekilde filtrelenmiştir. Bu veriler aşağıdaki kriterler kullanılarak daha da filtrelenmiştir:

1. (1)

   Numune değerleri, mineral ayrımlarının aksine tam rock jeokimyası ile ilgili olmalıdır.

2. (2)
   

   Bireysel örneğin ana eleman, iz elemanı olması gerekir, ⁸⁷SR/⁸⁶SR, ¹⁴³ND/¹⁴⁴Nd, ²⁰⁶PB/²⁰⁴PB, ²⁰⁷PB/²⁰⁴Pb ve ²⁰⁸PB/²⁰⁴PB izotop değerleri mevcuttur.

3. (3)

   Koordinatlar, daha geniş bir çalışma alanı için ortalama bir koordinat sağlamak yerine bireysel örneğin konumuna özgü olmalıdır.

Örnekleme ve örnek hazırlama

Uzaktaki çeşitli vokanlardan doksan üç lav, 11 kaynaklı tüf ve bir ponza örneği (Erta Ale vokanik segmenti, Ayelu, Abida, Yandud, Dama Ali, Kirub, Ela, Didoli, Abbahu, Tat Ali ve Manda Hararo) için seçildi.^50–51–52. Örnekler, 1960’larda uzaktaki CNR/CNRS projeleri sırasında toplandı.⁵³ ve İtalya’nın Pisa Üniversitesi’nde uzak depoda saklandı (http://reposities.dst.unipi.it/index.php/home-afar). Üç saha mevsiminde Boset -Bericha Volkanik Kompleksi’nden (BBVC) 52 örnek toplandı⁵⁴Kasım 2012’de, Nisan – Mayıs 2015⁵⁵ ve Şubat 2017⁵⁶.

Major, iz ve izotop analizleri için örnek hazırlama Southampton Üniversitesi’nde gerçekleştirildi. Numuneler, yıpranmış bölümleri çıkarmak için bir testere ile kesildi ve kesilmiş yüzeyler, testere bıçağından metallerin potansiyel kontaminasyonunu azaltmak için topraklandı. Kaya numuneleri daha sonra bir sinek pres kullanılarak ezildi ve ezme işlemi sırasında metal kontaminasyonunu en aza indirmek için ezilmeden önce çift katmanlı plastik torbalara yerleştirildi.

Ezilmiş malzeme, analiz için orta fraksiyonu (0.5-1 mm) tutarak Teflon elekleri kullanılarak üç boyutlu fraksiyonlara (> 1 mm, 0.5-1 mm, <0.5 mm) ayrıldı. Seçilen fraksiyon, Milli-Q su içinde ultrasonikleştirilerek temizlendi, daha sonra gece boyunca 85 ° C'de bir fırında kurutuldu. Daha sonra temizlenmiş kaya yongaları, herhangi bir yabancı (rock olmayan) malzemeyi uzaklaştırmak için bir mikroskop altında elle seçildi. Pb izotop analizi için temizlenmiş çiplerin bir kısmı kullanıldı. Ana eleman için, iz elemanı, ¹⁴³ND/¹⁴⁴Nd ve ⁸⁷SR/⁸⁶SR izotop analizi, kalan kaya cipsi, metallerle kontaminasyonu en aza indirmek için yine bir akik harç ve havaneli kullanılarak ince bir toza öğütüldü.

Eser eleman analizi

Örnekler, 0.05 g (BBVC numuneleri için) veya 0.075 g (diğer tüm numuneler için) toz numunesi kullanılarak tam rock iz elemanı analizi için hazırlandı. Toz örnekleri, 15 damla konsantre HNO ile kapalı savillex teflon şişeleriyle sindirildi₃ ve 24 saat boyunca 130 ° C’de (BBVC’den hariç tüm numuneler için) veya 50 damla HF ve 0.2 mL HNO ile bir ocakta 2 mL HF₃ 24 saat boyunca 130 ° C’de bir ocakta (sadece BBVC numuneleri için). HNO₃/HF buharlaştırıldı ve numuneler, 130 ° C’de bir ocakta 24 saat daha 6 m HC1 içerisinde geri akıtıldı. 6 M HC1 buharlaştırıldı ve numuneler 6 M HC1 içerisinde yeniden çözüldü. Anne çözeltileri, çözünmüş numunelere 6 M HC1 ve Milli-Q su (toplam 30 mL) ilave edilerek hazırlandı. Kızı çözeltileri,% 3 HNO ile 5 ml’ye kadar seyreltilmiş 0.5 ml anne çözeltisi kullanılarak hazırlandı.₃ (5 ppb içinde/5 ppb re/20 ppb içinde iç standartları içeren), ~ 4.000 genel bir seyreltme faktörü ile sonuçlanır.

Kızı örneklerinin eser eleman analizleri, Southampton Üniversitesi’nde Thermo Scientific X Serisi 2 Quadrupole indüktif olarak birleştirilmiş plazma kütle spektrometresi (ICP-MS) üzerinde gerçekleştirildi. Örnekler ve standartlar dahili standart öğelerle ekildi ve müdahaleler ve boşluk için düzeltildi ve daha sonra bir dizi uluslararası rock standartları kullanılarak kalibre edildi. Doğruluk, referans malzemeler JA-2, BCR-2 ve JB-2 (Ek Tablolar kullanılarak izlendi 1 Ve 2).

PB izotopik analiz

Pb izotop analizi için, 0.3 g temizlenmiş, toplanan kaya yongaları (0.5-1.0 mm) Pb savillex teflon şişelerine tartıldı ve numunenin tam olarak çözülmesini önlemek için 1 saat boyunca 4 ml 6 m HC1 (obsidiyen ve pumis numuneleri için 15 dakika) ile bir ocakta sızdırıldı. Numuneler milli-Q su içinde birkaç kez durulandı, ardından 0.5 mL konsantre HNO₃ 3-4 mL konsantre HF eklemeden önce. Örnekler, eser elementlerle aynı prosedürü izleyerek sindirildi ve kuruluk için buharlaşmadan önce 24 saat boyunca 130 ° C’de bir ocakta geri akma. Daha sonra 0.5 mL konsantre HC1 ilave edildi ve numune kuruluk için buharlaştırıldı. Daha sonra 0.5 mL konsantre HNO₃ ilave edildi ve tekrar kuruluk için buharlaştı. Son tortu 0.5 mL HBR içerisinde yeniden oluşturuldu ve 1 saat geri akıtıldı. Numuneler soğutuldu ve 5 dakika santrifüjlendi. Pb, tek aşamalı bir HC1 anyon değişim kromatografik reçine ayırma yöntemi kullanılarak izole edildi⁵⁷Agx-1 × 8, 200–400 Mesh Reçinesi ile. Bunu takiben, PB izolatı kurutuldu, HNO’da yeniden çözüldü₃ ve Ref. ⁵⁸. Örnekler daha sonra Southampton Üniversitesi’nde (İngiltere) Thermo Scientific Neptune çok kolektör endüktif olarak birleştirilmiş plazma kütle spektrometresi (MC-ICP-MS) üzerinde analiz edildi. ²⁰⁶PB/²⁰⁴Pb = 16.9404 ± 24 (142 ppm), ²⁰⁷PB/²⁰⁴Pb = 15.4969 ± 26 (168 ppm), ²⁰⁸PB/²⁰⁴Pb = 36.7149 ± 66 (180 ppm) (2 SD; N= 44). Standarın PB izotop ölçümleri, kabul edilen değerlerin hatasıdır (²⁰⁶PB/²⁰⁴PB = 16.9412, ²⁰⁷PB/²⁰⁴PB = 15.4988, ²⁰⁸PB/²⁰⁴Pb = 36.7233). Doğruluk 47 ppm idi ²⁰⁶PB/²⁰⁴Pb, 123 ppm için ²⁰⁷PB/²⁰⁴Pb ve 174 ppm için ²⁰⁸PB/²⁰⁴Pb.

¹⁴³ND/¹⁴⁴Nd ve ⁸⁷SR/⁸⁶SR izotopik analiz

SR ve ND analizi için, BBVC’ninki hariç tüm numuneler için eser eleman çözeltilerinin hazırlanmasından (önceki olana bakınız) kalan ana çözümler kullanılmıştır. Her bir anne çözeltisinin bir alikotu, en az 1 μg SR ve 200 ng nd içeren bir hacim sıvı vermek ve 130 ° C’de bir ocakta Savillex Teflon şişelerinde kuruluk için buharlaştırılmıştır. Numune kalıntıları 200 ul 1.75 M HC1 içerisinde yeniden oluşturuldu. BBVC numuneleri için kaya yongaları, Savillex Teflon şişelerinde 4 mL 6 m HC1 içinde 30 dakika süreyle sızdırıldı (numunenin tam olarak çözülmesini önlemek için sadece 15 dakika boyunca obsidiyen örnekler). Örnekler daha sonra mili-q su ve HNO ile durulandı₃ve daha sonra önceki eser eleman analizi ile aynı sindirim prosedürü izlendi. Son anne çözeltileri, felsik numuneler için 30 ml’ye HCL ve Milli-Q su kullanılarak hazırlandı ve mafik numuneleri için 20 mL.

Daha sonra tüm numuneler, SR ve ND fraksiyonlarını ayırmak için bir AG50-X8 200-400 Mesh Reçine katyon kolonu kullanılarak iyon değişim kolonu kimyasından geçirildi. Örnek fraksiyonlar daha sonra kuruyana kadar buharlaştırıldı, daha fazla sütun kimyası için hazırlandı.

SR, Ref. ⁵⁹. Numuneler daha sonra kuruyana kadar buharlaştırıldı, 1.5 mL 1 M HC1 içerisinde çözündürüldü ve 1 uL TA-aktivatör ile dışlanmış tantal filamentlerine yüklendi. SR izotopik analizi, Southampton Üniversitesi’nde bir termal iyonizasyon kütle spektrometresi termo bilimsel triton artı üzerinde gerçekleştirildi. Referans materyali srm nist987 (⁸⁷SR/⁸⁶SR = 0.710258; Georem) doğruluğu izlemek için kullanıldı ve ortalama verdi ⁸⁷SR/⁸⁶0.710243 SR değerleri. Tüm numuneler NBS SRM-987’ye normalleştirildi ⁸⁷SR/⁸⁶SR = 0.710248 (Ref. ⁶⁰), tekrarlanabilirlik ± 0.000020 (28.2 ppm, 2 SD; N = 464). Doğruluk 21 ppm idi.

Katyon kolonundan ND alikotunu bir LN-spec reçinesi (50-100 μm) izledi (Ref. ⁵⁹). Örnekler daha sonra kuruluk ve% 3 HNO’ya buharlaştırıldı₃ 50 ppb çözeltisi üretmek için eklendi. ¹⁴³ND/¹⁴⁴Southampton Üniversitesi’ndeki Termoscientific Neptune MC-ICP-MS üzerinde ND analizleri yapıldı. Düzeltilmiş ND izotopik bileşimler, ref. ⁶¹ Bir ayarlama yoluyla ¹⁴⁶ND/¹⁴⁴0.7219 ND oranı ve ikincil normalizasyon ¹⁴²ND/¹⁴⁴ND = 1.141876. Referans materyali JNDI-1 bilinmeyen olarak ölçüldü (¹⁴³ND/¹⁴⁴0.512124, 2 SD (Refs. ^62–63)), ortalama elde etmek ¹⁴³ND/¹⁴⁴2 yıl boyunca altı analiz seansında ± 0.000008 (2 SD, 15.2 ppm) harici tekrarlanabilirliği ile 0.512115 ND. Toplam sütun boşlukları (boş asit kolon prosedüründen çalıştırıldığında), SR ve ND için sırasıyla analiz edilen toplam miktarlara (1 ug ve 200 μg) kıyasla ihmal edilebilir (<20 pg).

v
_S eklem ters çevirisinden eşleme

Kullanıyoruz v_S Ref modeli. ³⁰ Analizimize dahil edilmek için. Üç boyutlu hız modeli, ortam gürültüsü ve teleseizmlerden Rayleigh-Wave faz hızlarının ortak ters çevrilmesi yoluyla oluşturulur.^30–64. . v_S Model, üst 50 km için 0.1 ° × 0.1 ° piksel boyutu ile her 5 km’de bir parametrelendirilir. Daha derin derinlikler için, Ref. ³⁸. Hız modelinin oluşturulması hakkında daha fazla bilgi için okuyucu Refs’e yönlendirilir. ^30–64 ve buradaki referanslar.

Bu makaledeki analiz için v_S Model, doğrusal bir enterpolasyon kullanılarak 1 km derinliğe enterpole edildi; Daha sonra, piksel boyutumuzla (0.1 ° × 0.1 °) aynı çözünürlükte derinlik ile tek boyutlu hız sütunlarını çıkardık.

Moho derinlikleri

Izgara moho derinlik haritası v_S Ref haritaları. ⁶⁴öncekinde açıklanmıştır. . v_S Model, 1 km dikey ızgara aralığına enterpolasyona tabi tutuldu. 3.75 km s’de bir hız dilimi^–1 Önceki alıcı işlev ölçümleriyle en iyi eşlenen kontur çıkarıldı^{65–66–67–68–69}aktif kaynak deneyleri (örneğin, ref. ⁴⁵) ve önceki s-dalga modelleri (örneğin, ref. ⁷⁰).

İstatistiksel modeller

Metinde açıklandığı gibi, beş model dikkate alındı ​​(genişletilmiş veri tablosu 2), her model doğrusal bir uyum ve bir spline uyumu kullanılarak test edilir (Şek. 3). En uygun çizgi ise, bir spline fitinin kendisinin doğrusal olabileceğini not ediyoruz.

Ampirik modeller, 14 jeokimyasal miktarın her birinin varyasyonu için tahmin edilmektedir (her biri rastgele değişken tarafından genel olarak temsil edilir Y ) mesafenin bir fonksiyonu olarak D ∈ [0, 1,800]Beş farklı model için KM. Modeller, varyasyonunu araştıran modeller Y ile D artan karmaşıklığı. En basit model (C1C), tek bir upwelling merkezinin (11.192 ° N, 41.784 ° E; Şek. 1 Ve 3), hangisi ile ilgili olarak D üç yarık için de tanımlanmıştır. Varyasyonu Y ile D tüm yarıklar için ortak varsayılır. Model C3C, üç yukarı çıkma merkezinin varlığını varsayar (11.192 ° N, 41.784 ° E; 14.008 ° N, 40.458 ° E; ve 6.626 ° N, 37.948 ° E; Şek. 1) Ref. ³⁶; Gözlemler en yakın upwelling merkezine tahsis edilir ve tek bir kişinin hesaplanmasını kolaylaştırır D Her gözlem için. Model C1C gibi Yile D yükselen tahsis ne olursa olsun, tüm yarıklarda ortak varsayılmaktadır. Model C1D D ama şimdi varyasyonu Yile D yarıklarda farklı olduğu varsayılır. Model C3D, tahmini için C3C’yi kopyalar D ama varyasyonu Y ile D yarıklarda farklı olduğu varsayılır. Son olarak, Model C3X’te, farklı varyasyonun varlığı ile üç yukarı çıkma merkezinin varlığını düşünüyoruz. Yile D her bir yukarı ve yarık kombinasyonu için.

Veri Ön İşleme

C1C ve C1D modelleri için, Abhe Gölü’ne (11.192170 ° N, 41.783750 ° e) merkezlenmiş her numune ile yukarı çıkma lokusu arasındaki mesafe hesaplanır. C3C, C3D ve C3X modelleri için, her bir numune ile üç yukarı çıkma konumunun her biri arasındaki mesafe (Şek. 1 Ve 3) ölçülür ve daha sonra her numune en yakın upwelling merkezine atanır. Mesafe (D ) iki konum arasında (upwelling ve örnek) küresel kosinüs yasası kullanılarak hesaplanır:

Neresi A Kuzey kutbundan örnek konuma açı (radyan cinsinden), B Kuzey Kutbu’ndan yükselen konuma açı (radyan cinsinden), C Numunenin boylam değerleri ile yükseliş arasındaki fark (radyanlarda) ve R metre cinsinden dünyanın yarıçapı mı (6.371 × 10³).

Cezalandırılmış B-SPLINES

Her model için varyasyonu Y ile D cezalandırılmış bir B-spline kullanılarak tarif edilir (örneğin Refs. ^71–72), özellikleri optimal öngörücü performans sağlamak için seçilir. Birincisi, mesafe alanında eşit aralıklı büyük bir dizin seti için, bir B-SPLINE temel matrisi hesaplıyoruz, B (Örneğin, ref. ⁷³)) P Eşit aralıklı kübik spline baz fonksiyonları. Sonra değeri YDizin setinde vektör tarafından verilir BB Spline katsayısı vektörü için B tahmin edilecek. Değeri P yüksek değişkenin iyi bir açıklamasını sağlamak için yeterince büyük olduğu belirtilmiştir. Y. Belirli bir veri kümesi için, ardışık değerler arasındaki farkı cezalandırırız. B Bir pürüzlü ceza kullanmak, böylece cezalandırılmış spline optimal pürüzlülük sergiler ve optimal öngörücü performans sağlar.

Optimal spline pürüzlülüğünü ve öngörücü performansı tahmin etmek

Bir örnek için N₁ Jeokimyasal ve jeofizik miktarların vektörlerinden oluşan eğitim verileri (y₁) ve mesafeler (D₁), önce her bir öğeyi tahsis ederiz D₁ Dizin setindeki en yakın komşusuna ve dolayısıyla uygun spline baz matrisini oluşturun B₁ örnek için. O zaman bunu varsayıyoruz ({ bf {y} _ {1}} = {b} _ {1} bf { upbeta} + bf { upepsilon} )unsurları nerede e bağımsız ve aynı dağılmış sıfır ortalama Gauss rastgele değişkenleridir. Pürüzlülüğü cezalandırıyoruz B İlk farklı bir ceza kullanmak LB ‘PBNeresi (P = d {^ prime} d ) Ve D birinci fark matrisidir (elementlerle (D} _ {ij} =-1 ) eğer (i = j ); (= 1 ) eğer (j = i+1 ); Ve (= 0 ) Aksi takdirde (örneğin, ref. ⁷⁴). Belirli bir seçim için ( lambda )sonra en uygun değerini buluyoruz B Uyum eksikliğini en aza indirerek:

Bir ayar kümesini kullanarak ortaya çıkan spline açıklamasının öngörücü performansını değerlendirebiliriz. N₂ Vektörler tarafından temsil edilen gözlemler (eğitim setinden bağımsız) y₂ Ve D₂. Uygun spline temel matrisini bularak tekrar başlıyoruz B₂ Bu örnek için. Ardından ayarlama örneği için öngörücü ortalama kare hatasını hesaplayabiliriz:

Bir dizi temsili değer seçeneğinin her biri için L . Daha sonra en uygun değerini seçebiliriz Lkullanma

Değer ({ text {MSE}} _ {{{ Mathrm {tune}}}} sol ({ lambda}^{*} right) ) değerinin değerinden beri önyargılı bir tahmini performansın önyargılı bir tahmini ({ lambda}^{*} ) değerini en aza indirmek için ayarlandı. Bir test seti kullanarak spline modelinin öngörücü performansı için tarafsız bir tahmin alabiliriz. N₃ Vektörler tarafından temsil edilen gözlemler (eğitim ve ayar setlerinden bağımsız) y₃ Ve D₃ (ve karşılık gelen spline baz matrisi B₃). Daha sonra öngörücü performans şu şekilde tahmin edilir:

Çapraz doğrulama ve model karşılaştırması

MSE’yi değerlendirmek için çapraz doğrulamadan yararlanıyoruz_Test veri örneğinin tamamını bölümleyerek K > Rastgele 2 grup, bir grubu ayarlama için stopaj ve kalanları test etmek ve tutmak için başka bir grup K– Eğitim için 2 grup. Daha sonra tren, ayar ve test gruplarının seçimi kombinasyonları üzerinde kapsamlı bir şekilde döneriz, tüm yinelemeler üzerinde test verilerindeki genel öngörücü performansı değerlendiririz, her gözlemin test setinde tam olarak bir kez meydana geldiğini belirtir. Verilerin alt kümelerine (C1D, C3D, C3X) ayrı model uyarlar gerektiren modeller için, MSE_Test her bir alt küme için optimal öngörücü modellerden tahminler kullanılarak tahmin edilir. Ayrıca, gözlemlerin farklı ilk rastgele bölümlemesi için analizi tekrarlayabiliriz. K Gruplar genel öngörücü performansın bu seçime duyarlılığını değerlendirmek. Öngörücü performansların adil bir şekilde karşılaştırılabilmesi için beş modelin her birini değerlendirmek için aynı çapraz doğrulama bölümlerini kullanmaya dikkat ediyoruz.

14 jeokimyasal miktarda model performansını ölçmek için ((J = Mathrm {1,2}, ldots, 13) )genel standartlaştırılmış MSE’yi tanımlıyoruz_Test

Nerede MSE_Test,J için öngörücü performans Jjeokimyasal gösterge ve (, {s} _ {j}^{2} ) bu miktarın varyansı için örnek tahminidir. Spline’ların tahmini ve öngörücü performanslarının test edilmesi 100’den fazla tekrarlandı. Her yinelemeden ve SMSE’nin ortalamasından elde edilen sonuçlar Şekil 2’de gösterilmiştir. 4.

Doğrusal regresyon

Karşılaştırma için, varyasyonu için doğrusal regresyon modellerini de değerlendiriyoruz. Yile D. Mevcut gösterimde, bunlar temel matrisli basit modeller olarak düşünülebilir. B=[1 d]Neresi 1 her eleman = 1 ile uygun uzunlukta bir vektördür. B Bu durumda, kesişme ve eğim katsayılarına karşılık gelen elementlere sahip 2 vektördür. Doğrusal regresyon, pürüzlülük katsayısı olarak cezalandırılmış B-spline modelleri kullanılarak yaklaşılır L→ ∞. Yani, doğrusal regresyon, çok büyük olan cezalandırılmış bir B-spline modeline karşılık gelir. L. Bu nedenle, cezalandırılmış bir B-spline modelinin en azından doğrusal regresyonun yanı sıra gerçekleştirmesi garanti edilir.

Model performansının belirsizliği

Belirsizliğin model performansı üzerindeki etkisini araştırmak için bir pertürbasyon analizi yapıldı. Bu analiz, üretilmesini ve modellenmesini gerektiriyordu. N_Peyze Yeni veri örnekleri. Bu veri örneklerinin her biri, orijinal veri örneğinin bozulmasına karşılık geldi. Bir değeri N_Peyze = 300, pertürbed verilerdeki öngörücü performans için% 95 belirsizlik bandının güvenle tahmin edilebileceğini sağlamak için seçildi.

Düzenli örnekte Q– ({q = 1,2, ldots, n} _ {{{ Mathrm {pert}}}} )değer ({y} {{{{u а ^ {}}) ki Ben değişken için gözlem J karşılık gelen değeri bozarak elde edildi (y} _ {ij}} ) Orijinal veri örneğinde, katkı maddesi Gauss gürültüsü kullanarak ({e} _ {{{e a □standart sapma ({ sigma} _ {{ij}} ) bunların değişkenin gözlemlenmesi için bilinen ölçüm belirsizliği değeri tarafından bilgilendirildi. Matematiksel olarak:

Tam modelleme prosedürü daha sonra her bozulmuş veri örneğine sırayla uygulandı. Farklı modellerin öngörücü performansı, N_PeyzeŞekil l’de gösterildiği gibi pertürbasyonlar. 4,% 95 belirsizlik bantları açısından. Şekil, C1D modelinin bozulmuş verilerde ve orijinal bozulmamış örnek için en iyi öngörücü performansı sağladığını göstermektedir. Pertürbasyon analizindeki gözlemlere gürültü eklendiğinden, pertürbed verilerdeki modellerin genel performansının beklendiği gibi orijinal numuneden daha zayıf olduğunu unutmayın.

Kabuk asimilasyonunun etkisini test etmek

CE/PB değerlerinin 20’nin altına düştüğü ve kabuk asimilasyonu ile ilişkili olabilecek durumları hariç tutarak kabuk asimilasyonunun etkisini daha da test ettik.^26–33. Ek analiz kullanarak, CE/Pb <20'nin genel sonuçlarımızı etkilemediği durumların hariç tutulması (Genişletilmiş Veri Şekil. 3a), birincil manto bileşimsel dalgalanmalarının (bileşimsel manto uç üyelerinin göreceli oranları) yüzeydeki patlayıcı bileşimler üzerinde birinci dereceden kontrolü uyguladığını düşündürmektedir.

PCA

PCA, her bir numunenin veya nesnenin her bir değişken için aynı sayıda değere sahip olmasını gerektirir, böylece veri kümesi 94 örneğe indirgenmiştir. PCA, incelenen manto uç üyeleri için verilerin mevcut olduğu numunelerin radyojenik izotop bileşimleri üzerinde gerçekleştirilir (Afar Tüy, Pan-Afrika litosfer, tükenmiş manto, Emi, Emi, Himu; Şekil. 5 ve genişletilmiş veri tablosu 3; Ref. ⁷⁵). Diğer tamamen jeokimyasal çalışmalar uzakta (örneğin Refs. ^14–37) Alt-kıtalaral litosfer manto gibi alt-kabuklu bileşenler eklediler, bu son üyeyi bazen belirli manto uç üyelerinden (EM1) ayırt edilemez, özellikle de alt-kıttal litosfer mantosunun metasomatize olduğu durumlarda dahil etmemeye karar verdik. Modellerimizdeki son üyeler için kullanılan tercih edilen değerler, genişletilmiş veri tablosunda verilmiştir 3. Her nesne PCA’ya dahil edilmeden önce standartlaştırılır:

Neresi ({ bar {y}} _ {j} ) değişkenin ortalamasıdır J Ve S_J değişkenin standart sapmasıdır J:

Neresi N_J Değişken içindeki nesne sayısıJ.

Varyansın yaklaşık% 90.5’i, ilk iki özvektörün düzleminde açıklanmakta ve üçüncü özvektör dahil ederken% 95.5’e yükselir. İlk ana bileşen (PC-1) en çok etkilenir ²⁰⁷PB/²⁰⁴Pb ve ²⁰⁸PB/²⁰⁴Pb, ikinci ana bileşen (PC-2) baskın olarak etkilenir ²⁰⁶PB/²⁰⁴Pb ve ⁸⁷SR/⁸⁶Üçüncü Ana Bileşen’e (PC-3) hakimdir. ²⁰⁷PB/²⁰⁴Pb ve ¹⁴³ND/¹⁴⁴ND (Ek Tablo 3).

K-ortalama küme analizi

K-ortalama küme analizi⁷⁶ 13 standart değişken kullanılarak numuneler üzerinde gerçekleştirildi (moho derinliği hariç; genişletilmiş veri tablosu 1; Refs. ^{77–78–79–80–75}). K-ortalama algoritması, her nesneyi başka bir (bölümsel kümelenme) ile örtüşmeyen tekil bir kümeye atar ve her bir kümenin merkez noktasından her bir veri noktasına kare hatalarının toplamını en aza indirir.

Optimum küme sayısını bulmak için ( K)-en düşük küme sayısına sahip kare hatalarının toplam toplamını azaltan-K-ortalama algoritmasını belirterek Kher biri için 1,000’den fazla yineleme 1/20 olmak K(Ek Şek. 1). Daha sonra dört kümeyi seçiyoruz. K= 4, karelerin toplam toplamını% 60 azaltmak K= 1 ve 1.000 yinelemenin üzerindeki aralık K≥ 4.. Her nesne için, 1.000 yinelemeden küme atamaları, bunun küme içi toplam kare toplamına en yakın yineleme numarasını bularak seçilir.KDeğer (Ek Şek. 1).